تعريف:
إذا كان رأس الزاوية هو الأصل ، فإن الزاوية تقع في الوضع القياسي للمستوى الديكارتي ، ويقع جوار البداية في الاتجاه الإيجابي للمحور x ، ويقع جوار النهاية على أحد الأرباع الأربعة أو المحور.
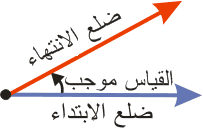
تعلمت أن الزاوية عبارة عن زوج من الأشعة لهما نفس نقطة البداية ، وتسمى هذه النقطة رأس الزاوية ، ويطلق على أحد الشعاعين نقطة بدء الزاوية ، ويسمى الشعاع الثاني بنقطة النهاية.
كما يتضح مما سبق ، فإن الشكل (ج) هو رسم تخطيطي يمثل الموضع القياسي للزاوية.
قياس الزاوية هو مقدار الدوران من جوار البداية لـ موضع انتهاء الإدخال. كما هو مبين في الشكلين ، إذا كان ضلع البداية يدور عكس اتجاه عقارب الساعة ، يكون موجبًا ؛ إذا تم تدويره عكس اتجاه عقارب الساعة ، يكون المقياس سالبًا.
 |
 |
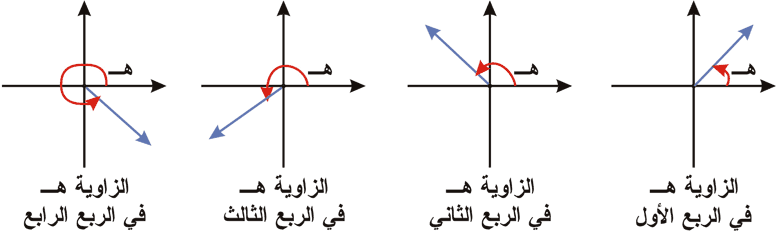
وتحدد من الموضع القياسي للزاوية في المستوى الديكارتي
نقول إذا كان صفر
|
180 درجة |
وفي الربع الثاني إذا كانت 90 درجة |
|
270 درجة |
إذا كانت 180 درجة |
|
360 درجة. |
إذا كان عند 270 درجة شرقًا |
مثال 1-:-
وضح في أي رباعي أو محور يكون الناحية النهائي لكل زاوية أدناه في موضعه القياسي.
أ) هـ = 120 ، ب) هـ = 60 ، ج) هـ = 225 ، د) هـ = 90.
ثم اسحبهم كافةًا لـ الوضع القياسي؟
لكن متى تكون الزاوية سالبة؟يعتمد ذلك على دوران جوار البداية ، إذا كان الدوران
يتطابق ضلع البداية مع اتجاه الدوران والزاوية سالبة وهو ما ذكرناه سابقًا.
مثال 2 -: –
كل زاوية أدناه موحدة على المستوى الديكارتي.
أ) -60 درجة ب) -150 درجة مئوية) -300 درجة.
لكن الآن ، هل لاحظت أن زاوية ضلع الزاوية الموجبة (60 درجة) هي نفس زاوية ضلع الزاوية السالبة (300)؟ أي أن الزاوية 60 درجة = -300 درجة.
لذلك ، ما نريد إيجاده هو أنه يمكن أن تكون هناك عدة زوايا في طرف انتهاء الموضع القياسي.
كافة الزوايا (E + N x 360 °) (n مجموعة صحيح) على الصورة لها نفس سطح انتهاء الصلاحية. بمعنى انتهاء ، الوجه النهائي للزاوية E في الموضع القياسي هو نفس الوجه النهائي للزاوية (E + N x 360 °) في الموضع القياسي.دعونا نوضح





