أهم معلومة عن قوانين حساب المثلثات

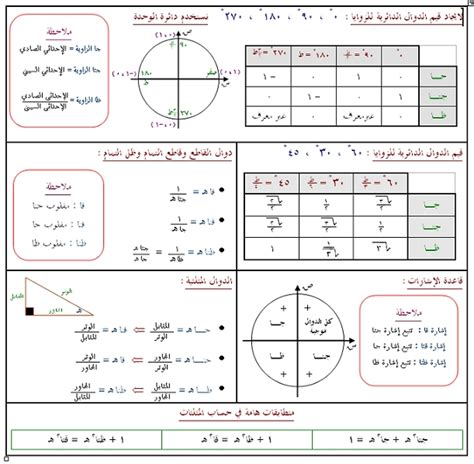
وسنستعرض معًا أهم المعلومات المتعلقة بقواعد علم المثلثات الذي يعتبر من أبرز فروع الرياضيات ومن النوع العام للهندسة. يعتمد هذا العلم على دراسة المثلثات والزوايا، بالإضافة إلى الدوال المثلثية مثل الجيب وجيب التمام.

تجدر الإشارة إلى أن قدماء المصريين هم أول من استخدم قوانين حساب المثلثات، حيث استخدمت في بناء الأهرامات والمعابد، بينما صاغ اليونانيون أول القوانين المتعلقة بمساحة الدائرة. وستوضح هذه الموسوعة مساهمة العلماء في تطوير هذا العلم ونجاحه في مختلف مجالات الحياة الواقعية، بالإضافة إلى شرح شامل لجميع القوانين ذات الصلة.

أهم المعلومات عن علم المثلثات

• كلمة “علم المثلثات” مشتقة من الكلمة اليونانية “trigonon” وتعني المثلث وأبعاده.
• علم المثلثات هو دراسة العلاقة بين زوايا وأضلاع المثلثات ويعتبر فرعا هاما من فروع الرياضيات.
• يتداخل علم المثلثات مع دراسة الدوال المتعلقة بالزوايا في المثلثات، مثل الجيب وجيب التمام والظل.
• يشمل علم المثلثات حساب الزوايا والمسافات بينها، وبالإضافة إلى حساب التفاضل والتكامل، فهو يتقاطع مع فروع الرياضيات الأخرى مثل اللوغاريتمات والأعداد المركبة.
• يتم تعريف جيب التمام على أنه طول الضلع المقابل للزاوية القائمة، في حين أن جيب التمام هو النسبة بين الجانب المجاور لزاوية معينة والوتر في المثلث القائم.

شخصية بارزة في تطوير علم المثلثات

1. ناصر الدين الطوسي: هو أول من جعل علم المثلثات علماً مستقلاً عن علم الفلك. وساعد في تطوير الدوال المثلثية وترجمت أعماله في أوروبا.
2. جيما فريسيوس: عالمة رياضيات هولندية يُنسب إليها كونها أول من أدخل طريقة التثليث التي تعتمد على قياس زوايا وأضلاع المثلث لإيجاد الإحداثيات والمسافات باستخدام نظرية الجيب.
3. ليونهارت أويلر: عالم رياضيات سويسري ساهم في تطوير استخدام الأعداد المركبة في علم المثلثات.
4. جيمس جريجوري: عالم رياضيات سويسري آخر لعب دورًا بارزًا في تحسين المتسلسلة المثلثية.

ما فائدة قانون المثلثات؟

لعلم المثلثات فوائد عديدة ويستخدم في مجالات متعددة مثل:

• تصنع أجهزة التلفاز وملاعب الكرة والأثاث.
• التدخل في بناء الطرق والمباني.
• يمكن استخدامه لحساب المسافات بين المدن والبلدان والقارات.
• تستخدم لعلم الفلك وأبحاث الأقمار الصناعية.
• المساهمة في صناعة المحركات.

ما هي قوانين علم المثلثات؟

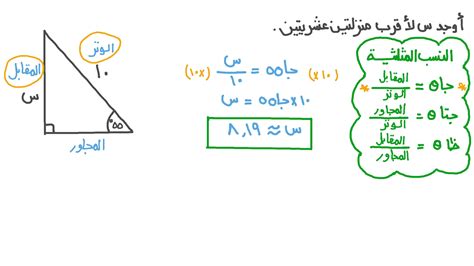
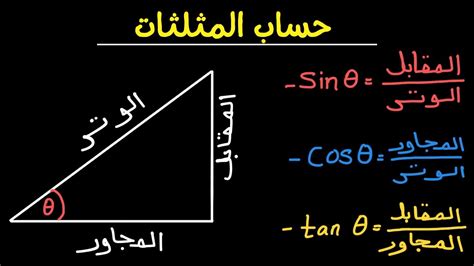
• Sin(x) = المقابل/الوتر.
• Cos(x) = المجاور/الوتر.
• tan(x) = sin(x) / cos(x).
• المهد(س) = 1/ظا(س).
• المهد(x) = cos(x) / الخطيئة(x).
• ف(س) = 1/كوس(س).
• Co(x) = 1/sin(x).
• Sin²(x) + cos²(x) = 1.
• قا² (س) = 1 + ظا² (س).
• سرير²(س) = 1 + سرير²(س).
• جيب (-x) = -جيب (x).
• كوس(-س) = كوس(س).
• تان(-x) = -تان(x).
• الخطيئة (90 – س) = جتا (س).
• cos(90 – x) = sin(x).
• تان (90 – س) = تان (س).
• جيب التمام (90 + س) = جيب التمام (س).
• جيب التمام (90+x) = -sin(x).
• ظا(90+س) = -سرير(س).
• الخطيئة (180 – س) = الخطيئة (س).
• كوس(180 – س) = -كوس(س).
• تان (180 – س) = -تان (س).
• جيب (180+س) = -جيب (س).
• cos(180 + x) = -cos(x).
• ظا(180 + س) = ظا(x).
• الخطيئة (360 – س) = – الخطيئة (س).
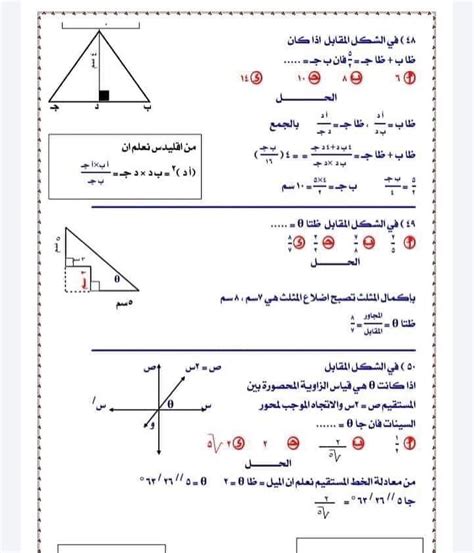
• كوس (360 – س) = كوس (س).
• ظا(360 – س) = – ظا(س).
• الخطيئة (360 + س) = الخطيئة (س).
• cos(360 + x) = cos(x).
• ظا(360 + س) = ظا(س).
• الخطيئة (أ + ب) = الخطيئة (أ) + جتا (ب) + جتا (أ) + خطيئة (ب).
• الخطيئة (أ – ب) = الخطيئة (أ) – جتا (ب) + جتا (أ) – الخطيئة (ب).
• cos(a + b) = cos(a) cos(b) – sin(a) sin(b).
• Cos(a – b) = cos(a) cos(b) + sin(a) sin(b).
• ظا(أ + ب) = (ظا(أ) + ظا(ب)) / (1 – (ظا(أ) ظا(ب))).
• ظا(أ – ب) = (ظا(أ) – ظا(ب)) / (1 + ظا(أ) ظا(ب)).
• الخطيئة(أ + ب) الخطيئة(أ – ب) = الخطيئة²(أ) – الخطيئة²(ب) = cos²(ب) – cos²(أ).
• Cos(a + b) = cos(a – b) = cos² (a) – cos² (b) = sin² (b) – sin² (a).
• ظا (45 + أ) = (1 + ظا (أ)) / (1 – ظا (أ)).
• ظا (45 – أ) = (1 – ظا (أ)) / (1 + ظا (أ)).
• 2 خطيئة(أ) جتا(ب) = خطيئة(أ + ب) + خطيئة(أ – ب).
• 2 cos(a) sin(b) = sin(a + b) – sin(a – b).
• 2 cos(a) cos(b) = cos(a + b) + cos(a – b).
• 2 الخطيئة (أ) الخطيئة (ب) = جتا (أ – ب) – جتا (أ + ب).